Lösung Abitur Bayern 2019 Mathematik Stochastik III

zur Angabe dieser Abituraufgabe

Teilaufgabe Teil A 2 (3 BE)

Die Zufallsgröße

X

kann ausschließlich die Werte 1, 4, 9 und 16 annehmen.
Bekannt sind

P (X = 9) = 0, 2

und

P (X = 16) = 0, 1

sowie der Erwartungswert

E (X) = 5

. Bestimmen Sie mithilfe eines Ansatzes für den Erwartungswert die Wahrscheinlichkeiten

P (X = 1)

und

P (X = 4)

Lösung zu Teilaufgabe Teil A 2

Erwartungswert einer Zufallsgröße

Mit

P (X = 1) = a

und

P (X = 4) = b

ergibt sich fogende Wahrscheinlichkeitsverteilung:

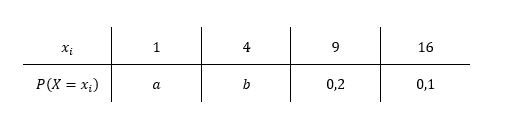
Es gilt:

P (X = 1) + P (X = 4) + P (X = 9) + P (X = 16) = 1

a + b + 0, 2 + 0, 1 = 1

a + b = 0, 7

(Gleichung I)

Weiterhin gilt:

E (X) = 5

Schritt einblenden / ausblenden

Erwartungswert einer Zufallsgröße

Nimmt eine Zufallsgröße

X

die Werte

x_{1}, x_{2}, \dots, x_{n}

jeweils mit den Wahrscheinlichkeiten

p_{1}, p_{2}, \dots, p_{n}

an, so gilt für den Erwartungswert dieser Zufallsgröße:

E (X) = \sum_{i = 1}^{n} x_{i} \cdot P (X = x_{i}) = x_{1} p_{1} + x_{2} p_{2} + \dots + x_{n} p_{n}

5 = 1 \cdot P (X = 1) + 4 \cdot P (X = 4) + 9 \cdot P (X = 9) + 16 \cdot P (X = 16)

5 = 1 \cdot a + 4 \cdot b + 9 \cdot 0, 2 + 16 \cdot 0, 1

5 = a + 4 b + 3, 4

a + 4 b = 1, 6

(Gleichung II)

Lineares Gleichungssysem aus I und II lösen:

\begin{matrix} I. & a + b = 0, 7 \\ II. & a + 4 b = 1, 6 \end{matrix}

II. - I.

a + 4 b - a - b = 1, 6 - 0, 7

\Leftrightarrow

3 b = 0, 9

\Rightarrow

b = 0, 3

b = 0, 3

in I. einsetzen:

a + 0, 3 = 0, 7

\Rightarrow

a = 0, 4

Gesuchte Warscheinlichkeiten:

P (X = 1) = 0, 4

P (X = 4) = 0, 3

Alle Abituraufgaben

Lösungen zu:

Teilaufgabe Teil A 1a

Teilaufgabe Teil A 1b

Teilaufgabe Teil A 2

Teilaufgabe Teil A 3

Teilaufgabe Teil B 1

Teilaufgabe Teil B 2a

Teilaufgabe Teil B 2b

Teilaufgabe Teil B 2c

Teilaufgabe Teil B 2d

Teilaufgabe Teil B 2e

Teilaufgabe Teil B 2f

Lösung als Video:

Lösung als Video

Themen dieser Aufgabe:

Erwartungswert einer Zufallsgröße

Themen-Übersicht

Tipp:

Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.

Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?