Lösung Abitur Bayern 2017 Mathematik Analytische Geometrie V

zur Angabe dieser Abituraufgabe

Teilaufgabe Teil A 1a (3 BE)

Gegeben sind die Punkte

A (2 | 1 | - 4)

B (6 | 1 | - 12)

und

C (0 | 1 | 0)

Weisen Sie nach, dass der Punkt

C

auf der Geraden

A B

, nicht aber auf der Strecke

[A B]

liegt.

Lösung zu Teilaufgabe Teil A 1a

Geradengleichung aufstellen

weitere Abituraufgaben zu diesem Thema

Richtungsvektor der Geraden

A B

\vec{A B} = \vec{B} - \vec{A} = (\begin{matrix} 6 \\ 1 \\ - 12 \end{matrix}) - (\begin{matrix} 2 \\ 1 \\ - 4 \end{matrix}) = (\begin{matrix} 4 \\ 0 \\ - 8 \end{matrix})

Schritt einblenden / ausblenden

Geradengleichung

Eine Gerade

g

ist durch einen Ortsvektor

\vec{P}

und einen Richtungsvektor

\vec{v}

eindeutig bestimmt:

g : \vec{X} = \vec{P} + μ \cdot \vec{v}

μ \in ℝ

Wenn

A

als Aufpunkt genommen wird, dann ist

\vec{A}

der Ortsvektor (des Aufpunkts) der Geraden

l

l : \vec{X} = \underset{\vec{A}}{\underset{︸}{(\begin{matrix} 2 \\ 1 \\ - 4 \end{matrix})}} + λ \cdot (\begin{matrix} 4 \\ 0 \\ - 8 \end{matrix})

Lagebeziehung Punkt und Gerade

weitere Abituraufgaben zu diesem Thema

Prüfen, ob

C

auf der Geraden

A B

liegt:

(\begin{matrix} 0 \\ 1 \\ 0 \end{matrix}) = (\begin{matrix} 2 \\ 1 \\ - 4 \end{matrix}) + λ \cdot (\begin{matrix} 4 \\ 0 \\ - 8 \end{matrix})

(\begin{matrix} - 2 \\ 0 \\ 4 \end{matrix}) = λ \cdot (\begin{matrix} 4 \\ 0 \\ - 8 \end{matrix})

\Rightarrow

{\begin{matrix} λ = - \frac{1}{2} \\ 0 = 0 \\ λ = - \frac{1}{2} \end{matrix}

\Rightarrow

C \in l

Lage des Vektors

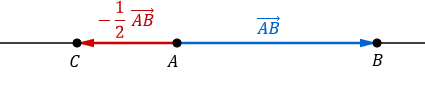
weitere Abituraufgaben zu diesem Thema

Wegen der Konstruktion der Geraden

A B

, kann

C

nicht auf der Strecke

A B

liegen, da man von

A

aus in negativer Richtung

(- \frac{1}{2} \cdot \vec{A B})

gehen muss, um zum Punkt

C

zu gelangen.

Alternative Lösung

weitere Abituraufgaben zu diesem Thema

\vec{C B} = \vec{B} - \vec{C} = (\begin{matrix} 6 \\ 1 \\ - 12 \end{matrix}) - (\begin{matrix} 0 \\ 1 \\ 0 \end{matrix}) = (\begin{matrix} 6 \\ 0 \\ - 12 \end{matrix})

\vec{A B} = (\begin{matrix} 4 \\ 0 \\ - 8 \end{matrix})

| \vec{C B} | > | \vec{A B} |

, kann

C

nicht auf der Strecke

A B

liegen.

Alle Abituraufgaben

Lösungen zu:

Teilaufgabe Teil A 1a

Teilaufgabe Teil A 1b

Teilaufgabe Teil A 2a

Teilaufgabe Teil A 2b

Teilaufgabe Teil B a

Teilaufgabe Teil B b

Teilaufgabe Teil B c

Teilaufgabe Teil B d

Teilaufgabe Teil B e

Teilaufgabe Teil B f

Lösung als Video:

Lösung als Video

Themen dieser Aufgabe:

Geradengleichung aufstellen

Lagebeziehung Punkt und Gerade

Lage des Vektors

Alternative Lösung

Themen-Übersicht

Tipp:

Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.

Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!