über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Lösung Abitur Bayern 2014 Mathematik Infinitesimalrechnung I
Teilaufgabe Teil B 3b (6 BE)
Ermitteln Sie die Gleichung der Tangente an im Punkt . Berechnen Sie den Wert, den das Modell für die Größe des Winkels liefert, den die Blattränder an der Blattspitze einschließen.
Lösung zu Teilaufgabe Teil B 3b
Tangentengleichung ermitteln
Tangentengleichung im Punkt :
Schritt einblenden / ausblenden
Nebenrechnungen:
Winkel zwischen zwei Geraden
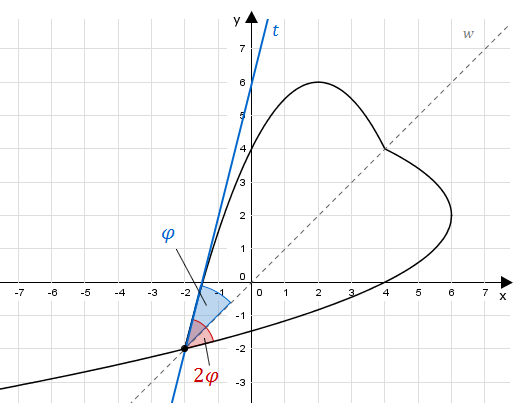
Betrachtet wird nun das Dreieck, welches von Ursprung, Blattspitze und -Achsenabschnitt der Tangente gebildet wird.
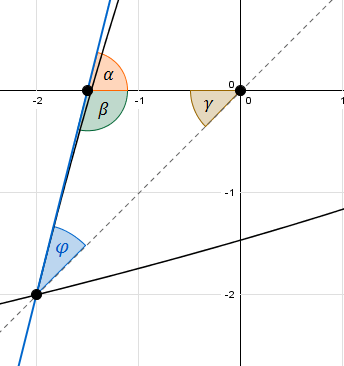
Neigungswinkel der Tangente gegen die -Achse bestimmen:

Neigungswinkel der Tangente gegen die -Achse bestimmen:
Schritt einblenden / ausblenden
Nebenwinkel zu :
Winkel an Ursprung:
Winkel Blattspitze:
Alternative Lösung
Richtungsvektor der Tangente :
Richtungsvektor der Winkelhalbierenden :
Richtungsvektor der Winkelhalbierenden :
Schritt einblenden / ausblenden
Schritt einblenden / ausblenden
Winkel Blattspitze:
Lösungen zu:
Themen dieser Aufgabe:
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?