Lösung Abitur Bayern 2013 Mathematik Stochastik IV

zur Angabe dieser Abituraufgabe

Teilaufgabe 1b (4 BE)

Zeigen Sie, dass

P_{J} (\bar{K}) > P_{\bar{J}} (\bar{K})

gilt.

Begründen Sie, dass es trotz der Gültigkeit dieser Ungleichung nicht sinnvoll ist, sich im Wahlkampf vorwiegend auf die Jungwähler zu konzentrieren.

Lösung zu Teilaufgabe 1b

Bedingte Wahrscheinlichkeit

weitere Abituraufgaben zu diesem Thema

Vierfeldertafel aus Teilaufgabe 1a:

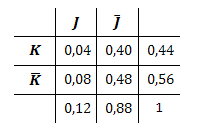
Schritt einblenden / ausblenden

Formel für die bedingte Wahrscheinlichkeit

P_{A} (B) = \frac{P (A \cap B)}{P (A)}

P_{J} (\bar{K}) = \frac{P (J \cap \bar{K})}{P (J)} = \frac{0, 08}{0, 12} \approx 0, 67

Schritt einblenden / ausblenden

Formel für die bedingte Wahrscheinlichkeit

P_{A} (B) = \frac{P (A \cap B)}{P (A)}

P_{\bar{J}} (\bar{K}) = \frac{P (\bar{J} \cap \bar{K})}{P (\bar{J})} = \frac{0, 48}{0, 88} \approx 0, 55

Somit gilt:

\underset{0, 67}{\underset{︸}{P_{J} (\bar{K})}} > \underset{0, 55}{\underset{︸}{P_{\bar{J}} (\bar{K})}}

Schritt einblenden / ausblenden

Es ist nicht sinnvoll sich im Wahlkampf vorwiegend auf die Jungwähler zu konzentrieren, da unter den nicht Jungwähler, die Anzahl der Unentschlossenen wesentlich größer ist.

Alle Abituraufgaben

Lösungen zu:

Teilaufgabe 1a

Teilaufgabe 1b

Teilaufgabe 1c

Teilaufgabe 2a

Teilaufgabe 2b

Teilaufgabe 3a

Teilaufgabe 3b

Teilaufgabe 3c

Lösung als Video:

Lösung als Video

Themen dieser Aufgabe:

Bedingte Wahrscheinlichkeit

Themen-Übersicht

Tipp:

Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.

Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!