über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern

Abitur 2011 G9 Abitur Mathematik GK Analytische Geometrie VI

Auf dem Boden des Mittelmeeres wurde ein antiker Marmorkörper entdeckt, der ersten Unterwasseraufnahmen zufolge die Form eines Pyramidenstumpfs besitzen könnte. Mithilfe eines Peilungssystem konnte die Lage von sieben der acht Eckpunkte ermittelt und zur weiteren Analyse des Körpers in einem kartesischen Koordinatensystem modellhaft dargestellt werden:
A ( 0 | 0 | 0 ) , B ( - 6 | - 12 | 12 ) und C ( 18 | - 36 | 0 ) sind Eckpunkte der Grundfläche, A ′ ( 14 | - 8 | 8 ) , B ′ ( 12 | - 12 | 12 ) , C ′ ( 20 | - 20 | 8 ) und D ′ ( 22 | - 16 | 4 ) die Eckpunkte der Deckfläche (vgl. Abbildung).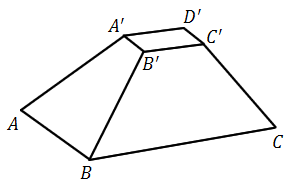
Teilaufgabe 1a  (5 BE)
Zeigen Sie, dass die Deckfläche A ′ B ′ C ′ D ′ ein Rechteck ist und den Inhalt 72 besitzt.

Teilaufgabe 1b  (3 BE)
Weisen Sie nach, dass das Dreieck A B C bei B rechtwinklig ist, und bestimmen Sie die Koordinaten des Punkts D , der gemeinsam mit A , B und C die Eckpunkte eines Rechtecks bildet.

Exakte Messungen am Marmorkörper zeigen, dass der Punkt D im Modell die Lage des vierten Eckpunkts der Grundfläche beschreibt.
Teilaufgabe 1c  (8 BE)
Bestimmen Sie eine Gleichung der Ebene E , die die Grundfläche A B C D enthält, in Normalenform. Weisen Sie nach, dass die Deckfläche parallel zur Grundfläche ist und von dieser den Abstand 12 hat.

[mögliches Teilergebnis: E : 2 x 1 + x 2 + 2 x 3 = 0 ]


Durch Berechnungen wird bestätigt, dass der Marmorkörper die Form eines Pyramidenstumpfs hat. Im Modell wird für weitere Überlegungen auch die zum Stumpf gehörige Pyramide mit Grundfläche A B C D betrachtet.
Teilaufgabe 1d  (6 BE)
Berechnen Sie die Höhe h dieser Pyramide.

[Ergebnis: h = 18 ]



Teilaufgabe 1e  (5 BE)
Bestimmen Sie das Volumen des Pyramidenstumpfs.

Teilaufgabe 1f  (8 BE)
Auf besonderes Interesse stößt die Seitenfläche des Marmorkörpers, die im Modell mit B C C ′ B ′ bezeichnet wurde. Zeigen Sie, dass die Geraden B C und B ′ C ′ den Abstand 6 5 besitzen und berechnen Sie den Inhalt dieser Seitenfläche im Modell.

Teilaufgabe 1g  (5 BE)
Um Informationen über den inneren Aufbau des Marmorkörpers zu erhalten, wird er geradlinig durchbohrt - im Modell betrachtet parallel zur x 3 -Achse, ausgehend vom Mittelpunkt der Kante [ B B ′ ] . Berechnen Sie im Modell die Koordinaten des Punkts, in dem die Bohrung aus der Grundfläche austritt.

Alle Abituraufgaben
Lösungen zu:
Teilaufgabe 1a
Teilaufgabe 1b
Teilaufgabe 1c
Teilaufgabe 1d
Teilaufgabe 1e
Teilaufgabe 1f
Teilaufgabe 1g
Lösung als Video:
Themen-Übersicht
Themen
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!