über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Lösung Abitur Bayern 2011 G8 Musterabitur Mathematik Stochastik IV
Teilaufgabe 2a (4 BE)
Man liest gelegentlich, dass eine nach rechts geneigte Handschrift einen Hinweis auf Aufgeschlossenheit darstellt. In einer Abteilung mit Angestellten gelten als aufgeschlossen. der als aufgeschlossen geltenden Angestellten haben eine Handschrift, die nicht nach rechts geneigt ist. Weiter ist bei Angestellten, die nicht als aufgeschlossen gelten, die Handschrift nach rechts geneigt.
Die Ereignisse : "Ein zufällig ausgewählter Angestellter hat eine nach rechts geneigte Handschrift" und : "Ein zufällig ausgewählter Angestellter gilt als aufgeschlossen" sollen auf stochastische Abhängigkeit untersucht werden.
Die Ereignisse : "Ein zufällig ausgewählter Angestellter hat eine nach rechts geneigte Handschrift" und : "Ein zufällig ausgewählter Angestellter gilt als aufgeschlossen" sollen auf stochastische Abhängigkeit untersucht werden.
Stellen Sie die beschriebene Situation in einem vollständig beschrifteten Baumdiagramm oder in einer vollständig ausgefüllten Vierfeldertafel dar.
Lösung zu Teilaufgabe 2a
Bedingte Wahrscheinlichkeit
Ereignisse:
: "Ein zufällig ausgewählter Angestellter gilt als aufgeschlossen"
: "Ein zufällig ausgewählter Angestellter hat eine nach rechts geneigte Handschrift"
Aus der Einleitung der Teilaufgabe 2a:
"In einer Abteilung mit 50 Angestellten gelten 35 als aufgeschlossen"
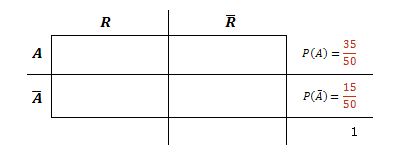
" der als aufgeschlossen geltenden Angestellten haben eine Handschrift, die nicht nach rechts geneigt ist."
: "Ein zufällig ausgewählter Angestellter gilt als aufgeschlossen"
: "Ein zufällig ausgewählter Angestellter hat eine nach rechts geneigte Handschrift"
Aus der Einleitung der Teilaufgabe 2a:
"In einer Abteilung mit 50 Angestellten gelten 35 als aufgeschlossen"

" der als aufgeschlossen geltenden Angestellten haben eine Handschrift, die nicht nach rechts geneigt ist."
Schritt einblenden / ausblenden
Schritt einblenden / ausblenden
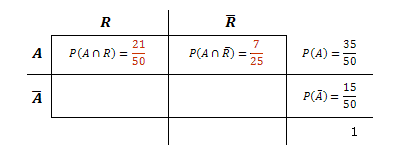
"Weiter ist bei 6 Angestellten, die nicht als aufgeschlossen gelten, die Handschrift nach rechts geneigt."
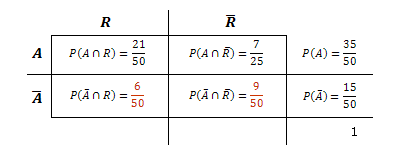
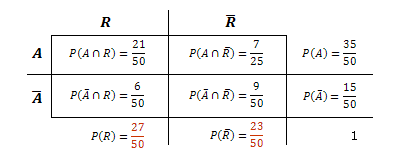
Alternative Lösung
Bei der Variante Baumdiagramm benötigt man die Wahrscheinlichkeiten und .
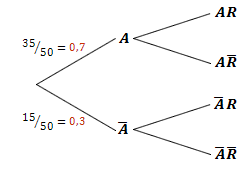
Zu dem werden alle 4 bedingten Wahrscheinlichkeiten benötigt.
Gegeben:
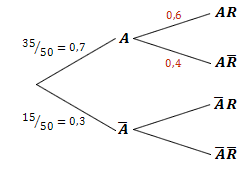
Gegeben:
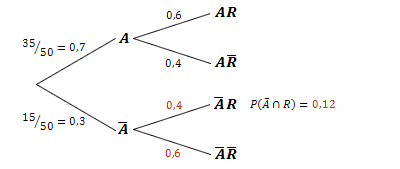
Die fehlendenden Schnittwahrscheinlichkeiten können dann mit der 1. Pfadregel bestimmt werden.

Zu dem werden alle 4 bedingten Wahrscheinlichkeiten benötigt.
Gegeben:

Gegeben:

Die fehlendenden Schnittwahrscheinlichkeiten können dann mit der 1. Pfadregel bestimmt werden.
Schritt einblenden / ausblenden

ergibt sich als Summe der Schnittwahrscheinlichkeiten und .
kann dann über das Gegenereignis berechnet werden.
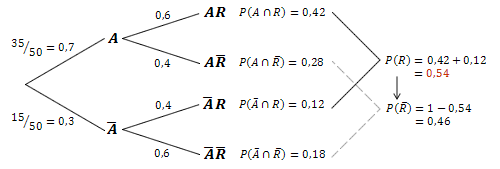
Lösungen zu:
Themen dieser Aufgabe:
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?








