über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Abitur 2011 G8 Musterabitur Mathematik Infinitesimalrechnung II
Teilaufgabe Teil 1 1 (5 BE)
Geben Sie für die Funktionen mit den folgenden Termen jeweils die maximale Definitionsmenge an und untersuchen Sie die Funktionen auf Nullstellen.
, ,
, ,
Teilaufgabe Teil 1 2 (5 BE)
Es gibt genau eine Tangente an den Graphen der Funktion , , deren Neigungswinkel gegen die -Achse beträgt. Bestimmen Sie eine Gleichung dieser Tangente.
Der Graph einer auf definierten, integrierbaren Funktion sei punktsymmetrisch zum Ursprung.
Teilaufgabe Teil 1 3a (3 BE)
Begründen Sie allgemein, dass dann für alle gilt: .
Teilaufgabe Teil 1 3b (4 BE)
Wählen Sie selbst eine Funktion , deren Graph punktsymmetrisch zum Ursprung ist, und bestätigen Sie für dieses die Aussage aus Teilaufgabe 3a, indem Sie das Integral für die gewählte Funktion mithilfe einer Stammfunktion berechnen.
Teilaufgabe Teil 1 4 (3 BE)
Welcher der angegebenen Terme nähert die Funktion für große Werte von am besten? Machen Sie Ihre Antwort plausibel.
(i) (ii) (iii) (iv) (v)
(i) (ii) (iii) (iv) (v)
Die Funktion wird im Definitionsbereich betrachtet. Der Graph von wird mit bezeichnet.
Teilaufgabe Teil 2 5a (10 BE)
Bestimmen Sie das Verhalten von an den Grenzen von .
Zeigen Sie, dass genau einen Hochpunkt besitzt, und berechnen Sie dessen Koordinaten.
Berechnen Sie und skizzieren Sie mit Hilfe der bisherigen Ergebnisse.
Zeigen Sie, dass genau einen Hochpunkt besitzt, und berechnen Sie dessen Koordinaten.
Berechnen Sie und skizzieren Sie mit Hilfe der bisherigen Ergebnisse.
[Zur Kontrolle: Hochpunkt an der Stelle ]
Teilaufgabe Teil 2 5b (3 BE)
Im Intervall besitzt genau eine Nullstelle . Führen Sie mit dem Startwert den ersten Schritt des Newton-Verfahrens zur näherungsweisen Berechnung von durch.
Man erhält dadurch auf zwei Dezimalen genau.
Man erhält dadurch auf zwei Dezimalen genau.
[Ergebnis: ]
Teilaufgabe Teil 2 5c (5 BE)
Berechnen Sie mithilfe des Näherungswerts aus Teilaufgabe 5b den Inhalt des Flächenstücks, das im I. Quadranten mit der -Achse einschließt.
Teilaufgabe Teil 2 5d (5 BE)
Betrachtet wird die Funktion , .
Beschreiben Sie den Verlauf des Graphen von in der Nähe des Punktes . Begründen Sie Ihre Ausführungen.
Welche Bedeutung hat das Ergebnis der Teilaufgabe 5c für die Funktion ?
Beschreiben Sie den Verlauf des Graphen von in der Nähe des Punktes . Begründen Sie Ihre Ausführungen.
Welche Bedeutung hat das Ergebnis der Teilaufgabe 5c für die Funktion ?
Jeder Körper sendet elektromagnetische Strahlung unterschiedlicher Frequenzen aus. Die Intensität der Strahlung hängt von der Frequenz der Strahlung ab. Im Idealfall gilt nach Max Planck für diese Intensität bei einem Körper der Temperatur :
, .
Dabei entspricht bis auf eine Konstante der Frequenz der Strahlung und der Parameter (Temperatur in Kelvin) ist positiv.
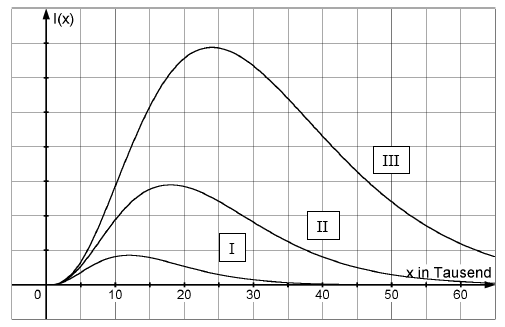
Die Graphik zeigt die zu drei Werten des Parameters gehörenden Graphen von .
Jede Scharfunktion hat genau eine Maximalstelle .
In den folgenden Teilaufgaben kann ohne Einheiten gerechnet werden.
, .
Dabei entspricht bis auf eine Konstante der Frequenz der Strahlung und der Parameter (Temperatur in Kelvin) ist positiv.
Die Graphik zeigt die zu drei Werten des Parameters gehörenden Graphen von .
Jede Scharfunktion hat genau eine Maximalstelle .

In den folgenden Teilaufgaben kann ohne Einheiten gerechnet werden.
Teilaufgabe Teil 2 6a (3 BE)
Weisen Sie am Funktionsterm nach, dass stets positiv ist.
Teilaufgabe Teil 2 6b (6 BE)
Weisen Sie nach, dass für die erste Ableitung der Funktion gilt:
Vergleichen Sie diesen Term mit dem der Funktion aus Aufgabe 5 und zeigen Sie, dass für die Maximalstelle von gilt: , wobei die positive Nullstelle von ist.
Vergleichen Sie diesen Term mit dem der Funktion aus Aufgabe 5 und zeigen Sie, dass für die Maximalstelle von gilt: , wobei die positive Nullstelle von ist.
Teilaufgabe Teil 2 6c (5 BE)
Unsere Sonne liefert maximale Intensität für (gelbgrüner Farbbereich). Welche Oberflächentemperatur ergibt sich hieraus für die Sonne?
Ordnen Sie die gezeichneten Graphen der Funktionsschar den Temperaturen Kelvin, Kelvin und Kelvin zu. Begründen Sie Ihre Antwort.
Ordnen Sie die gezeichneten Graphen der Funktionsschar den Temperaturen Kelvin, Kelvin und Kelvin zu. Begründen Sie Ihre Antwort.
Teilaufgabe Teil 2 6d (3 BE)
Ein Körper der Temperatur liefert für die Intensität . Begründen Sie, dass sich verachtfacht, wenn ein Körper mit doppelt so hoher Temperatur betrachtet wird.
Lösungen zu:
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?








