über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Abitur 2011 G8 Musterabitur Mathematik Infinitesimalrechnung I
Teilaufgabe Teil 1 1 (3 BE)
Bestimmen Sie die Nullstellen der Funktion mit Definitionsbereich .
Teilaufgabe Teil 1 2 (6 BE)
Gegeben ist die Funktion mit maximalem Definitionsbereich .
Geben Sie an und bestimmen Sie die Gleichung der Tangente an den Graphen von an der Stelle .
Geben Sie an und bestimmen Sie die Gleichung der Tangente an den Graphen von an der Stelle .
Teilaufgabe Teil 1 3 (3 BE)
Geben Sie den Term einer gebrochen-rationalen Funktion an, die die beiden folgenden Bedingungen erfüllt:
- Der Graph von berührt an der Stelle die -Achse.
- hat als Polstelle.
Teilaufgabe Teil 1 4 (3 BE)
Bestimmen Sie den Term einer Stammfunktion der Funktion , .
Teilaufgabe Teil 1 5 (5 BE)
Für sind die Funktionen mit den folgenden Termen gegeben:
, , mit
Ordnen Sie die Funktionen den nachfolgenden Graphen zu und bestimmen Sie die Parameter und . Erklären Sie Ihr Vorgehen.
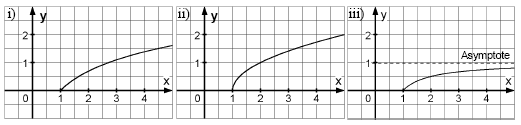
, , mit
Ordnen Sie die Funktionen den nachfolgenden Graphen zu und bestimmen Sie die Parameter und . Erklären Sie Ihr Vorgehen.

Gegeben ist die Funktion mit .
Teilaufgabe Teil 2 6a (2 BE)
Zeichnen Sie den Graphen in ein Koordinatensystem.
Teilaufgabe Teil 2 6b (6 BE)
Dem Flächenstück, das mit der -Achse einschließt, werden Rechtecke so einbeschrieben, dass jeweils eine Rechteckseite auf der -Achse liegt. Berechnen Sie den größtmöglichen Flächeninhalt eines solchen Rechtecks.
[Ergebnis: ]
[Ergebnis: ]
Teilaufgabe Teil 2 6c (5 BE)
Berechnen Sie, wie viel Prozent des Flächenstücks, das mit der -Achse einschließt, vom Rechteck maximalen Flächeninhalts aus Teilaufgabe 6b bedeckt werden.
Gegeben sind die Funktionen , , und , . Der Graph von ist für im nachfolgenden Diagramm dargestellt.
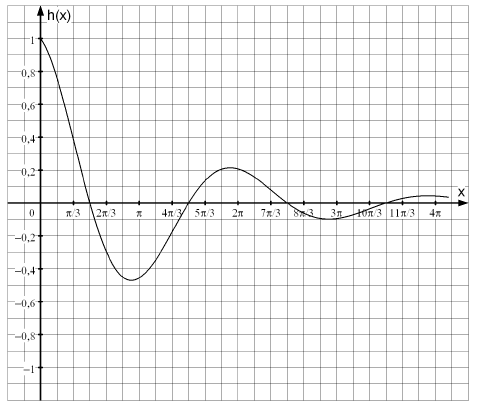

Teilaufgabe Teil 2 7a (8 BE)
Untersuchen Sie das Monotonieverhalten von und geben Sie das Verhalten von für und an.
Berechnen Sie die Funktionswerte , , , , und und zeichnen Sie damit die Graphen von und von in obiges Koordinatensystem ein.
Berechnen Sie die Funktionswerte , , , , und und zeichnen Sie damit die Graphen von und von in obiges Koordinatensystem ein.
Teilaufgabe Teil 2 7b (3 BE)
Die Funktion entsteht aus der Kosinusfunktion , , durch Multiplikation mit der Funktion . Beschreiben Sie, inwiefern sich der Graph von aufgrund dieser Multiplikation vom Graph der Kosinusfunktion unterscheidet. Gehen Sie dabei auch auf die Nullstellen von und die Funktionswerte , ein.
Teilaufgabe Teil 2 7c (6 BE)
Berechnen Sie den Term der ersten Ableitung von und weisen Sie nach, dass für Extremstellen von gilt: . Zeigen Sie damit, dass die Extremstellen von gegenüber den Extremstellen der Kosinusfunktion verschoben sind.
Teilaufgabe Teil 2 7d (4 BE)
Entscheiden Sie, ob die folgenden Aussagen I und II wahr oder falsch sind, und machen Sie Ihre Antworten plausibel:
Teilaufgabe Teil 2 7e (3 BE)
Die Funktion , , ist Stammfunktion von .
Zeigen Sie durch Rechnung, dass positiv ist, und deuten Sie diesen Zusammenhang am Graph von .
Zeigen Sie durch Rechnung, dass positiv ist, und deuten Sie diesen Zusammenhang am Graph von .
Teilaufgabe Teil 2 7f (3 BE)
Es gibt Werte , für die negativ ist. Geben Sie einen solchen Wert an und begründen Sie Ihre Wahl ohne Rechnung.
Lösungen zu:
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?








