über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
 
 
 
 
Lösung Abitur Bayern 2009 Mathematik GK Infinitesimalrechnung II


 
Teilaufgabe 3b  (5 BE)
F : x ↦ ( - x - 1 ) ⋅ e 2 - x mit x ∈ ℝ ist eine Stammfunktion von f (Nachweis nicht erforderlich).
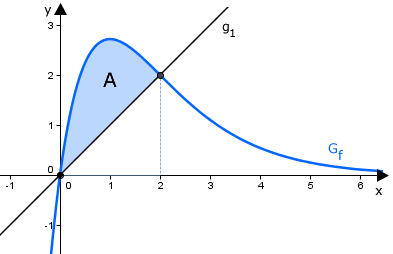
Ermitteln Sie den Inhalt der Fläche, die G f mit der Geraden g a für a = 1 einschließt.
 
Lösung zu Teilaufgabe 3b

Fläche zwischen zwei Funktionsgraphen





F ( x ) = ( - x - 1 ) ⋅ e 2 - x , x ∈ ℝ

g 1 ( x ) = x
Schritt einblenden / ausblenden
a = 1 ⇒ x S = 2 - ln 1 = 2 (siehe Teilaufgabe 3a)
Schritt einblenden / ausblenden
A = ∫ 0 2 ( f ( x ) - x ) d x
Schritt einblenden / ausblenden
= ∫ 0 2 f ( x ) d x - ∫ 0 2 x d x
Schritt einblenden / ausblenden
= [ F ( x ) ] 0 2 - [ 1 2 x 2 ] 0 2

= [ ( - x - 1 ) ⋅ e 2 - x ] 0 2 - [ 1 2 x 2 ] 0 2

= [ ( - 2 - 1 ) ⋅ e 2 - 2 - ( - 0 - 1 ) ⋅ e 2 - 0 ] - [ 1 2 2 2 - 1 2 0 2 ] 0 2

= - 3 ⋅ e 0 + e 2 - 2 + 0

= e 2 - 5

≈ 2 , 39

Themen-Übersicht
Themen
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?