über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Lösung Abitur Bayern 2009 Mathematik GK Infinitesimalrechnung II
Teilaufgabe 2b (6 BE)
Betrachtet wird die Integralfunktion für .
Bestimmen Sie ohne Verwendung einer integralfreien Darstellung der Funktion Art und Lage des Extrempunkts des Graphen von . Skizzieren Sie unter Einbeziehung der bisherigen Ergebnisse, insbesondere auch der Näherungswerte aus Teilaufgabe 2a, den Graphen von in das Koordinatensystem aus Teilaufgabe 1d.
Bestimmen Sie ohne Verwendung einer integralfreien Darstellung der Funktion Art und Lage des Extrempunkts des Graphen von . Skizzieren Sie unter Einbeziehung der bisherigen Ergebnisse, insbesondere auch der Näherungswerte aus Teilaufgabe 2a, den Graphen von in das Koordinatensystem aus Teilaufgabe 1d.
Lösung zu Teilaufgabe 2b
Art und Lage des Extrempunkts einer Integralfunktion
mit
Erste Ableitung bestimmen:
Erste Ableitung bestimmen:
Schritt einblenden / ausblenden
Erste Ableitung Null setzen:
(siehe Teilaufgabe 1a)
Schritt einblenden / ausblenden
Vorzeichen der ersten Ableitung bestimmen:
Schritt einblenden / ausblenden
Die Funktion ist für streng monoton steigend.
Schritt einblenden / ausblenden
Die Funktion ist für streng monoton fallend.
Schritt einblenden / ausblenden
Die Funktion hat an der Stelle ein Minimum.
-koordinate des Extrempunktes bestimmen:
-koordinate des Extrempunktes bestimmen:
Schritt einblenden / ausblenden
Minimum
Skizze
Aus Teilaufgabe 2a:
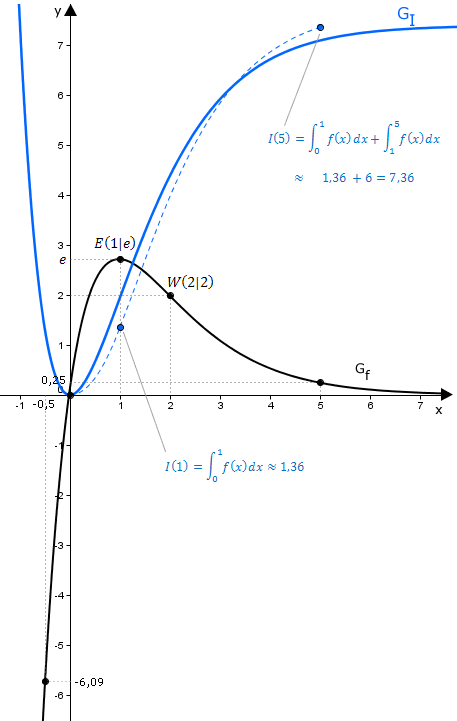
Bemerkung:
Die durchgezogene blaue Linie stellt den tatsächlichen Graphen der Integralfunktion dar. Die gestrichelte Linie stellt ein Teil des Graphen der Integralfunktion dar, der in der Aufgabe gezeichnet wird wenn man die Ergebnisse aus Teilaufgabe 2a berücksichtig

Bemerkung:
Die durchgezogene blaue Linie stellt den tatsächlichen Graphen der Integralfunktion dar. Die gestrichelte Linie stellt ein Teil des Graphen der Integralfunktion dar, der in der Aufgabe gezeichnet wird wenn man die Ergebnisse aus Teilaufgabe 2a berücksichtig
Lösungen zu:
Themen dieser Aufgabe:
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?








