über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
 
 
 
 
Lösung Abitur Bayern 2008 Mathematik GK Infinitesimalrechnung I


 
Teilaufgabe 1e  (7 BE)
Die Funktion F : x ↦ 4 ln ( x 2 + 4 ) mit D F = ℝ ist Stammfunktion von f (Nachweis nicht erforderlich).
Der Graph von f und der Graph der Umkehrfunktion g schließen im ersten Quadranten ein Flächenstück ein. Berechnen Sie den Inhalt A dieses Flächenstücks.
 
Lösung zu Teilaufgabe 1e

Fläche zwischen zwei Funktionsgraphen



f ( x ) = 8 ⋅ x x 2 + 4 , D f ∈ ℝ

F ( x ) = 4 ⋅ ln ( x 2 + 4 ) , D F ∈ ℝ

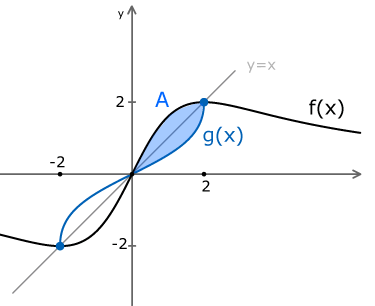
Flächeninhalt A bestimmen:
Schritt einblenden / ausblenden
A = ∫ 0 2 ( f - g ) ( x ) d x
Schritt einblenden / ausblenden
= 2 ⋅ ∫ 0 2 ( f ( x ) - x ) d x
Schritt einblenden / ausblenden
= 2 ⋅ [ F ( x ) - x 2 2 ] 0 2

= 2 ⋅ [ 4 ⋅ ln ( x 2 + 4 ) - x 2 2 ] 0 2
Schritt einblenden / ausblenden
= 2 ⋅ [ ( 4 ln 8 - 2 ) - ( 4 ln 4 - 0 ) ]

= 2 ⋅ ( 4 ln 8 - 4 ln 4 - 2 )

≈ 1 , 54

Themen-Übersicht
Themen
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?