Lösung Abitur Bayern 2005 Mathematik GK Infinitesimalrechnung II

zur Angabe dieser Abituraufgabe

Teilaufgabe 1a (6 BE)

Im Eingangsbereich eines Unternehmens soll das Firmenlogo im Boden eingelassen werden. Abb. 1 zeigt den Entwurf des Architekten nach Wahl eines geeigneten Koordinatensystems:

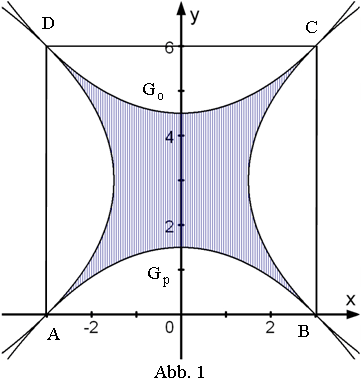
Im Quadrat ABCD schneiden vier kongruente parabelförmige Bögen die in Abb. 1 schraffierte Figur aus. Die untere Parabel

G_{p}

ist der Graph der quadratischen Funktion p mit

D_{p} = R

G_{p}

schneidet die x-Achse in den Punkten A(-3|0) und B(3|0). Die Diagonalen des Quadrats sind zugleich Tangenten an die Parabeln in den Punkten A und C bzw. B und D.

Geben Sie die Werte der Ableitung von p in den beiden Nullstellen an und bestimmen Sie den Funktionsterm der Funktion p.
[Zur Kontrolle:

p (x) = - \frac{1}{6} x^{2} + 1, 5

]

Lösung zu Teilaufgabe 1a

Funktionsgleichung ermitteln

weitere Abituraufgaben zu diesem Thema

p (x) = {ax}^{2} + bx + c

Schritt einblenden / ausblenden

allgemeine quadratische Funktion

Die Normalform der allgemeinen quadratischen Funktion lautet

x \mapsto {ax}^{2} + bx + c

\neq

0). Ihr Graph ist eine Parabel.
Durch quadratische Ergänzung erhält man die Scheitelform

x \mapsto a (x - x_{S}) + y_{S}

aus der man den Scheitelpunkt

S (x_{S} | y_{S})

ablesen kann.
Für

x = x_{S}

wird der Funktionswert minimal, falls a > 0 oder maximal, falls a > 0.

Beispiel:

y = 1, 5 x^{2} - 6 x + 5

Normalform

y = 1, 5 (x^{2} - 4 x + 3 \frac{1}{3})

y = 1, 5 (x^{2} - 4 x + 2^{2} - 2^{2} + 3 \frac{1}{3})

quadratische Ergänzung

y = 1, 5 [{(x - 2)}^{2} - \frac{2}{3}]

y = 1, 5 {(x - 2)}^{2} - 1

Scheitelform

a = 1,5 > 0 → S(2|-1) als Minimum

p'(x) = 2ax + b

Schritt einblenden / ausblenden

Erste Ableitung

f (x) = x^{n} \Rightarrow f' (x) = n · x^{n - 1}

Die gesuchte Parabel verläuft durch die Punkte A(-3|0) und B(3|0). Außerdem sind die Diagonalen des Quadrats Tangenten an die Parabel.

I: A ∈ p → p(-3) = 0 also: 0 = 9a - 3b + c
II: B ∈ p → p(3) = 0 also: 0 = 9a + 3b + c

Schritt einblenden / ausblenden

Erläuterung

Liegt der Punkt

P (p_{1} | p_{2})

auf

G_{f}

gilt:

f (p_{1}) = p_{2}

III: Steigung in A: p'(-3) = 1 → 1 = -6a + b
IV: Steigung in B: p'(3) = -1 → -1 = 6a + b

Schritt einblenden / ausblenden

Steigung eines Funktionsgraphen

Die Steigung eines Funktionsgraphen in einem Punkt ist gleich der Steigung der Tangenten an den Graph der Funktion in diesem Punkt.
Für die Steigung gilt:

m = f' (x_{0}) = tan α

Für diese Aufgabe gilt:

Steigung in A: m = tan 45

^{\circ}

= 1
also p'(-3) = 1

Setzt man diesen Sachverhalt in die Ableitung der allgemeinen Gleichung (p'(x) = 2ax + b) ein, erhält man
p'(-3) = 2·a·(-3) + b = 1

→ -6a + b = 1

Steigung in B: m = tan 135

^{\circ}

= -1
also p'(3) = -1

Setzt man diesen Sachverhalt in die Ableitung der allgemeinen Gleichung (p'(x) = 2ax + b) ein, erhält man
p'(3) = 2·a·3 + b = -1

→ 6a + b = -1

III: 1 = -6a + b
IV: -1 = 6a + b

III + IV: 0 = 2b → b = 0

b in III: 1 = -6a

\Rightarrow a = - \frac{1}{6}

a = - \frac{1}{6}

; b = 0 in I:

0 = 9 · (- \frac{1}{6}) - 3 · 0 + c

0 = - \frac{3}{2} + c

c = \frac{3}{2}

a = - \frac{1}{6}; b = 0; c = \frac{3}{2}

p (x) = {ax}^{2} + bx + c

\Rightarrow p (x) = - \frac{1}{6} x^{2} + \frac{3}{2}

Alle Abituraufgaben

Lösungen zu:

Teilaufgabe 1a

Teilaufgabe 1b

Teilaufgabe 2a

Teilaufgabe 2b

Teilaufgabe 2c

Teilaufgabe 3a

Teilaufgabe 3b

Teilaufgabe 3c

Lösung als Video:

Lösung als Video

Themen dieser Aufgabe:

Funktionsgleichung ermitteln

Themen-Übersicht

Tipp:

Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.

Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!