Lösung Abitur Bayern 2003 Mathematik LK Stochastik IV

zur Angabe dieser Abituraufgabe

Teilaufgabe 1b (4 BE)

Begründen Sie, dass die Stabdiagramme der Binomialverteilungen mit p = 0,5 achsensymmetrisch sind. Geben Sie die Symmetrieachse an.

Lösung zu Teilaufgabe 1b

Binomialverteilung

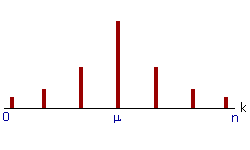
weitere Abituraufgaben zu diesem Thema

Zeichnung: achsensymmetrisches Stabdiagramm

Schritt einblenden / ausblenden

Binomialverteilung für n Versuche

Das Stabdiagramm einer Verteilung ist achsensymmetrisch, wenn gilt:

P_{p}^{n} (Z = k) = P_{p}^{n} (Z = n - k)

Binomialverteilung mit p=q=0,5:

P_{p}^{n} (Z = k) = (\begin{matrix} n \\ k \end{matrix}) \cdot 0, 5^{k} · 0, 5^{n - k}

P_{p}^{n} (Z = k) \overset{!}{=} P_{p}^{n} (Z = n - k)

linke Seite der Gleichung:

P_{p}^{n} (Z = k)

= (\begin{matrix} n \\ k \end{matrix}) \cdot 0, 5^{k} · 0, 5^{n - k}

= (\begin{matrix} n \\ k \end{matrix}) \cdot 0, 5^{k + n - k}

= (\begin{matrix} n \\ k \end{matrix}) \cdot 0, 5^{n}

rechte Seite der Gleichung:

P_{p}^{n} (Z = n - k)

= (\begin{matrix} n \\ n - k \end{matrix}) \cdot 0, 5^{n - k} · 0, 5^{n - (n - k)}

Schritt einblenden / ausblenden

Definition "k aus n"

Definition:

(\begin{matrix} n \\ k \end{matrix}) = \frac{n!}{k! · (n - k)!}

= \frac{n!}{(n - k)! · (n - (n - k))!} · 0, 5^{n}

= \frac{n!}{(n - k)! · k!} · 0, 5^{n}

= (\begin{matrix} n \\ k \end{matrix}) \cdot 0, 5^{n}

Beide Seiten der Gleichung liefern den gleichen Term. Also ist die Behauptung wahr.

Das Symmetriezentum ist der Erwartungswert E.

Bei einer binomialverteilten Zufallsgröße gilt:

E = n · p = μ

p = 0, 5 \Rightarrow μ = \frac{n}{2}

.

Das Stabdiagramm einer Binomialverteilung mit p = 0,5 ist achsensymmetrisch zu

k = \frac{n}{2}

Alle Abituraufgaben

Lösungen zu:

Teilaufgabe 1a

Teilaufgabe 1b

Teilaufgabe 1c

Teilaufgabe 1d

Teilaufgabe 2

Teilaufgabe 3a

Teilaufgabe 3b

Teilaufgabe 3c

Teilaufgabe 3d

Lösung als Video:

Lösung als Video

Themen dieser Aufgabe:

Binomialverteilung

Themen-Übersicht

Tipp:

Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.

Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!