über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern

Lösung Abitur Bayern 2003 Mathematik GK Infinitesimalrechnung I

zur Angabe dieser Abituraufgabe
Teilaufgabe 2a  (8 BE)
Gegeben ist nun zusätzlich die Funktion h : x ↦ 1 f ( x ) mit D h = ℝ . Ihr Graph wird mit G h bezeichnet.
Geben Sie die Wertemenge von h an und bestimmen Sie die Schnittpunkte von G f und G h .
Zeichnen Sie mit Hilfe der bisherigen Ergebnisse den Graphen G h im Bereich - 1 , 5 ≤ x ≤ 1 , 5 in das obige Koordinatensystem ein.
 
Lösung zu Teilaufgabe 2a
Wertebereich bestimmen



Der höchste Punkt von f ( x ) ist sein Maximum E ( 0 | e ) , d.h. der kleinste Wert den die Funktion h ( x ) annimmt ist:

h ( x E ) = 1 e 1 - 0 2 = 1 e

Da f ( x ) gegen 0 geht für x → ± ∞ , folgt dass h ( x ) gegen + ∞ geht für x → ± ∞

⇒ W h = [ 1 e , + ∞ [ Wertebereich von h ( x )
Schnittpunkt zweier Funktionen



Die Funktionen gleich setzen:

f ( x ) = h ( x ) ⇔ 1 e 1 - x 2 = e 1 - x 2 ⇔ e - ( 1 - x 2 ) = e 1 - x 2

Da die Basis ( e ) gleich ist, müssen die Exponenten gleich sein:

⇒ - ( 1 - x 2 ) = 1 - x 2 ⇔ - 1 + x 2 = 1 - x 2

⇒ 2 x 2 = 2

⇒ x 2 = 1

⇒ x 1 , 2 S = ± 1

⇒ y 1 , 2 S = f ( x 1 , 2 S ) = h ( x 1 , 2 S ) = e 1 - ( ± 1 ) 2 = e 0 = 1

⇒ S 1 ( 1 | 1 ) und S 2 ( - 1 | 1 ) sind Schnittpunkte von f und h
Skizze



Alle Abituraufgaben
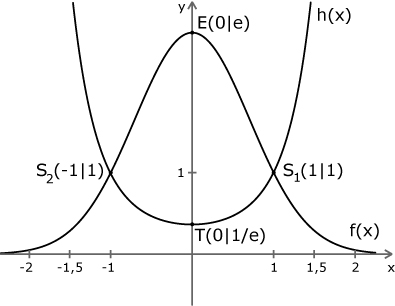
Lösungen zu:
Teilaufgabe 1a
Teilaufgabe 1b
Teilaufgabe 1c
Teilaufgabe 2a
Teilaufgabe 2b
Teilaufgabe 2c
Teilaufgabe 2d
Lösung als Video:
Lösung als Video
Themen dieser Aufgabe:
Wertebereich bestimmen
Schnittpunkt zweier Funktionen
Skizze
Themen-Übersicht
Themen
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!