über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Abitur 2010 Mathematik GK Infinitesimalrechnung II
Gegeben ist die Funktion mit dem Definitionsbereich . Der Graph von wird mit bezeichnet.
Teilaufgabe 1a (5 BE)
Untersuchen Sie das Verhalten von an den Rändern des Definitionsbereichs und geben Sie die Gleichungen der Asymptoten von an.
Teilaufgabe 1b (4 BE)
Die Terme der gebrochen-rationalen Funktionen und haben den gleichen Zähler wie , aber jeweils einen anderen Nenner. Geben Sie je einen möglichen Funktionsterm für und an, so dass im jeweils maximalen Definitionsbereich gilt:
- Der Graph von hat keine senkrechte Asymptote.
- Die Funktion hat an der Stelle eine Polstelle ohne Vorzeichenwechsel.
Teilaufgabe 2a (5 BE)
Geben Sie die Koordinaten der Achsenschnittpunkte von an und untersuchen Sie das Monotonieverhalten von .
Teilaufgabe 2b (4 BE)
Berechnen Sie und . Zeichnen Sie sowie die Asymptoten unter Verwendung der bisherigen Ergebnisse in ein Koordinatensystem ein.
Teilaufgabe 3 (4 BE)
Die Funktion ist umkehrbar (Nachweis nicht erforderlich). Bestimmen Sie den Term der Umkehrfunktion von . Was lässt sich aus dem Ergebnis hinsichtlich der Symmetrie von folgern?
Teilaufgabe 4a (3 BE)
Bestätigen Sie, dass die Funktion für eine Stammfunktion von ist.
Teilaufgabe 4b (5 BE)
Weisen Sie durch Rechnung nach, dass im I. Quadranten den Viertelkreis um den Koordinatenursprung mit Radius 1 in zwei etwa inhaltsgleiche Teilflächen zerlegt.
Die Ergebnisse der Aufgaben 1 bis 3 können im Folgenden verwendet werden.
Eine Kugel der Masse 1 kg bewegt sich nach rechts und stößt mit der Geschwindigkeit elastisch und zentral auf eine gleich große ruhende Kugel .
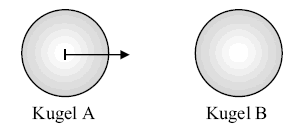
Die Maßzahl der Geschwindigkeit der Kugel in unmittelbar nach dem Zusammenstoß wird durch die Funktion mit beschrieben, wobei für die Maßzahl der Masse der Kugel in kg steht. Zu einer Bewegung nach rechts gehören positive Geschwindigkeiten, zu einer Bewegung nach links negative Geschwindigkeiten.

Die Maßzahl der Geschwindigkeit der Kugel in unmittelbar nach dem Zusammenstoß wird durch die Funktion mit beschrieben, wobei für die Maßzahl der Masse der Kugel in kg steht. Zu einer Bewegung nach rechts gehören positive Geschwindigkeiten, zu einer Bewegung nach links negative Geschwindigkeiten.
Teilaufgabe 5a (5 BE)
Berechnen Sie, mit welcher Geschwindigkeit sich Kugel unmittelbar nach dem Stoß bewegt, wenn die Masse der Kugel 0,6 kg beträgt.
Geben Sie die Grenzwerte der Funktion für sowie an und machen Sie für diese beiden Grenzfälle jeweils den Bewegungsablauf der Kugel im Sachzusammenhang plausibel.
Geben Sie die Grenzwerte der Funktion für sowie an und machen Sie für diese beiden Grenzfälle jeweils den Bewegungsablauf der Kugel im Sachzusammenhang plausibel.
Teilaufgabe 5b (5 BE)
Ermitteln Sie, für welche Werte von sich Kugel unmittelbar nach dem Stoß nach rechts bewegt.
Berechnen Sie, für welchen Wert von sich die Kugel unmittelbar nach dem Stoß mit nach links bewegt.
Berechnen Sie, für welchen Wert von sich die Kugel unmittelbar nach dem Stoß mit nach links bewegt.
Lösungen zu:
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?








